QExtend——XCTF

函数主逻辑

主逻辑

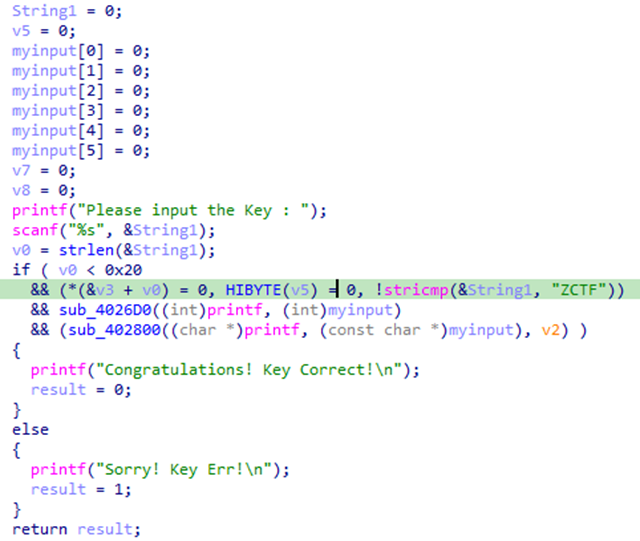
开始函数的逻辑，标记的一行为将输入的第四位和最后一位都变成0，即去掉flag中的{}，然后比较前四位是否位ZCTF，最后再使用flag中{}中的字符串。

sub_4026D0函数

进入loc_4026D0可以看到，这其实应该是一个函数，但被数据断开了，但经过不更改代码的调试发现0x4026E5的数据在之后会被用到，因此如果要程序正常执行就不能直接使用nop将其覆盖。

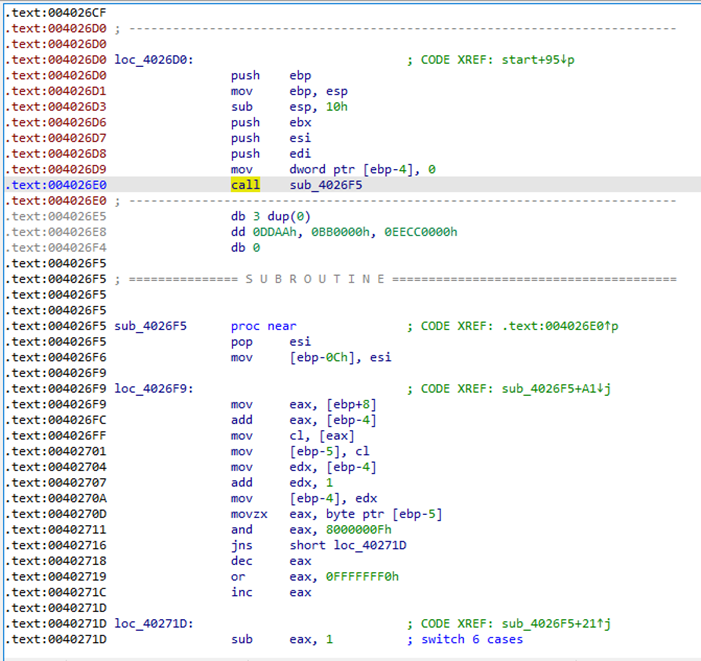
sub_4026D0汇编代码

先忽略这个数据，使用nop覆盖。

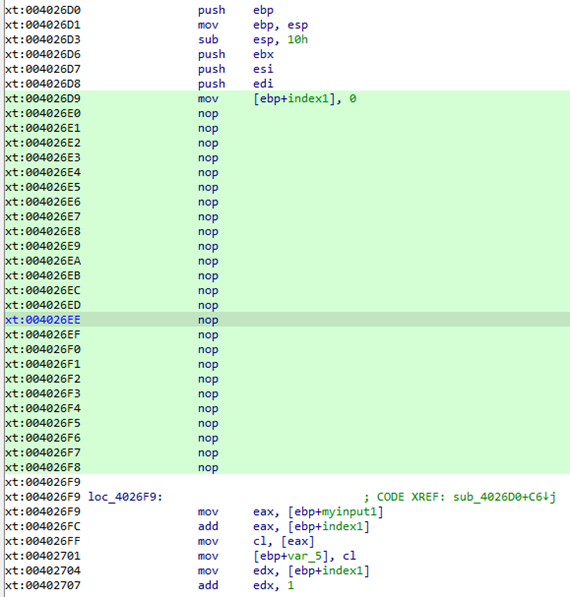
nop后的汇编代码

获得sub_4026D0函数的主要逻辑。

sub_4026D0函数主要逻辑

再进入switch的各个case的函数中看一下。

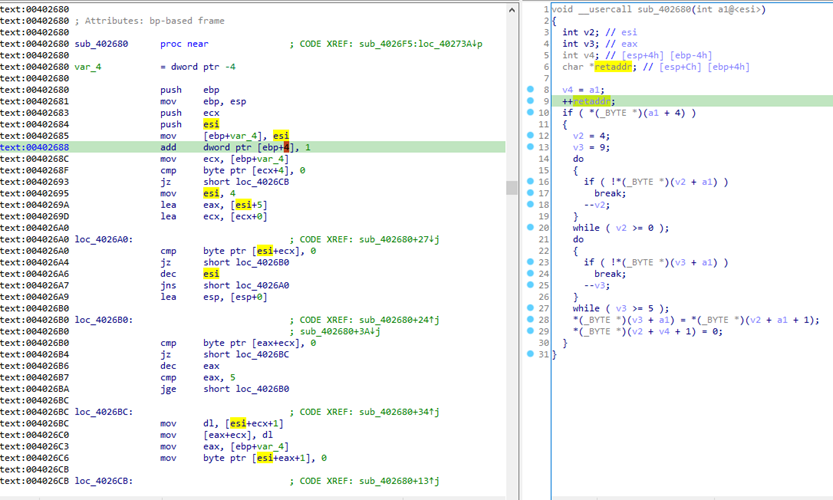
sub_4026D0函数的case0中的函数

这里被标记的行有将函数返回地址进行加一的操作，可以将其nop掉，因为函数返回地址处的指令没有啥作用。

回看被nop的数据

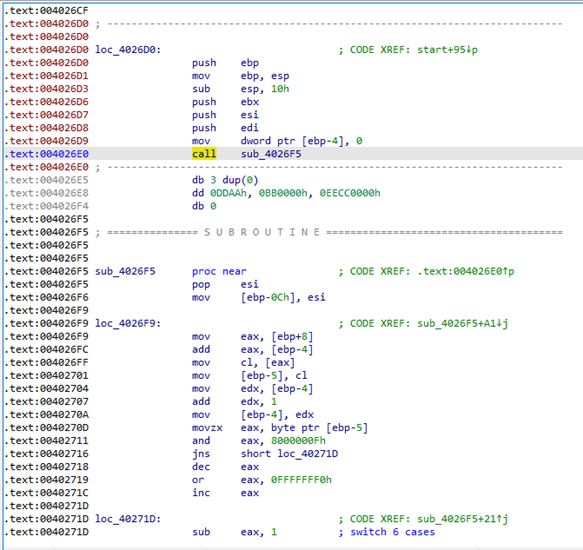
hanoi数据

此处的call会将函数返回地址压入栈中，而返回地址0x4026E5就是数据的地址，通过这种方法，当跳入sub_4026F5函数时，使用pop就可以获得数据的地址，然后继续下方的指令。

sub_4026F5函数没有push ebp；mov ebp esp；环节因此，第一个出栈的就是函数返回地址。

调用函数时的栈情况

此处将数据的地址pop到esi中，而且还使用mov [ebp-0Ch]，esi;将数据地址复制到一个参数上。esi到switch的各case的函数中之前都没有更改，因此各case中的函数直接使用esi来获取数据。

获取数据

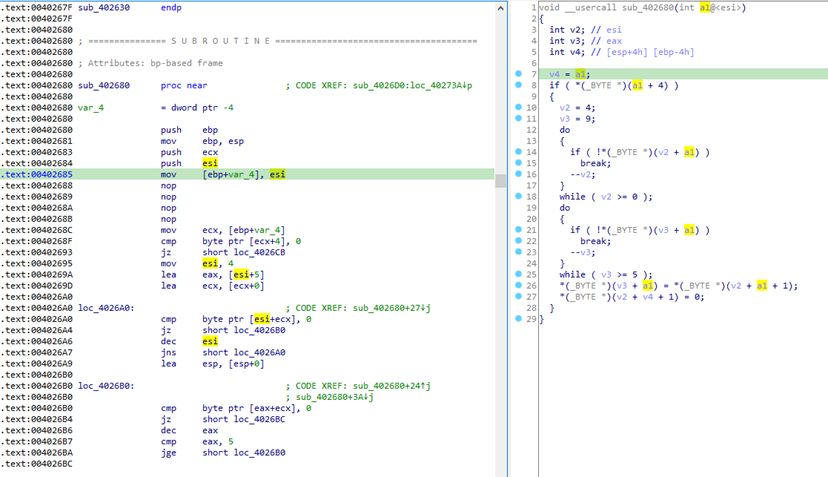
图中esi的位置就是指向数据的地址，函数直接使用。

switch各case中的函数的逻辑。

因为这里看了别的师傅的wp，因此知道这是一个hanoi游戏。

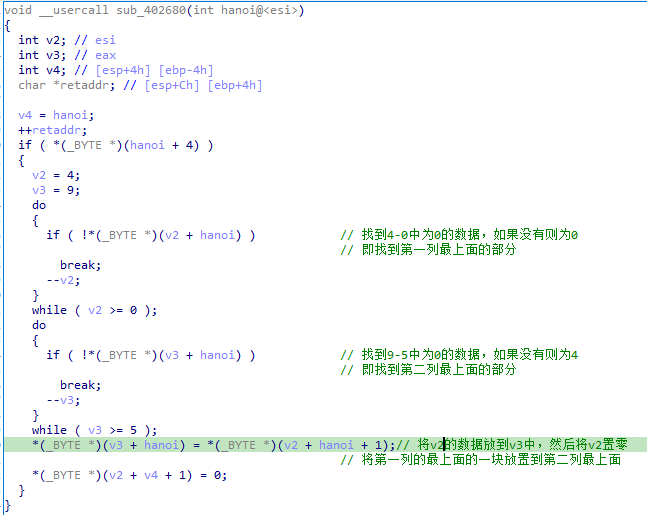
case中函数的逻辑

其他case中的函数，大差不差。

6个case分别对应这hanoi游戏中三列的互相移动。

switch存在与0xF相与再减一的操作（看汇编或者未nop的程序逻辑）。

switch

看if中的函数sub_402490，这是检查每一步操作是否符合hanoi规则的。

检验函数

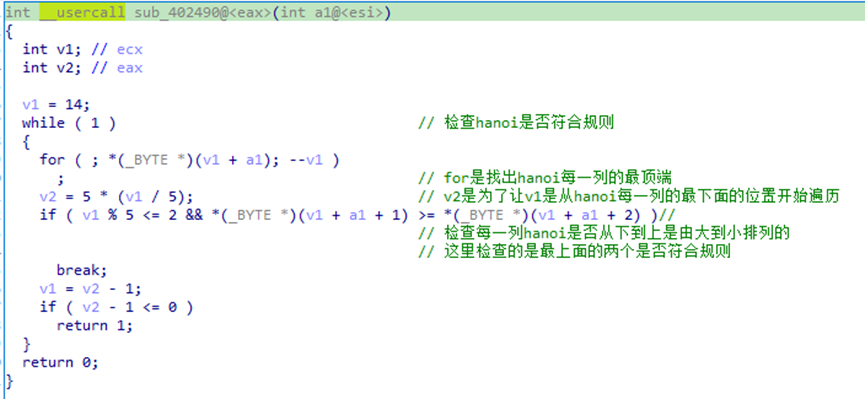
sub_4026F5的返回值。

返回值

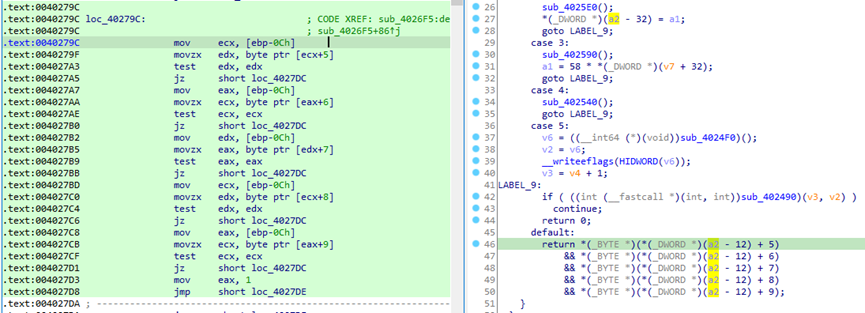
对比汇编和伪代码。可以看出a2就是[ebp-0Ch]，上面说过这是某数据的地址，这里获取了数据的第5、6、7、8、9位，再将它们进行&&运算，将结果作为返回值。

返回值

sub_402800函数。

汇编代码

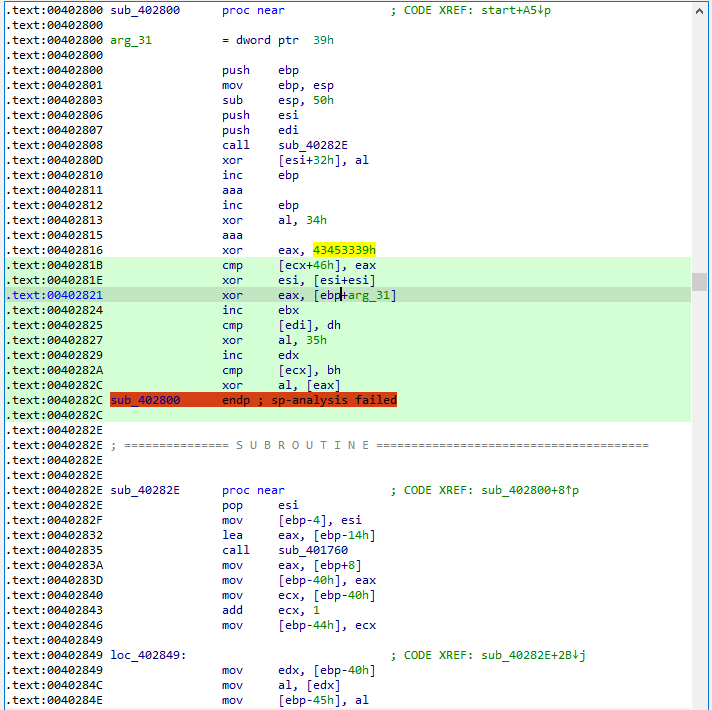
可以看出它与下方的sub_40282E其实应该是连在一起的。

现在看着汇编进行分析。

堆调用

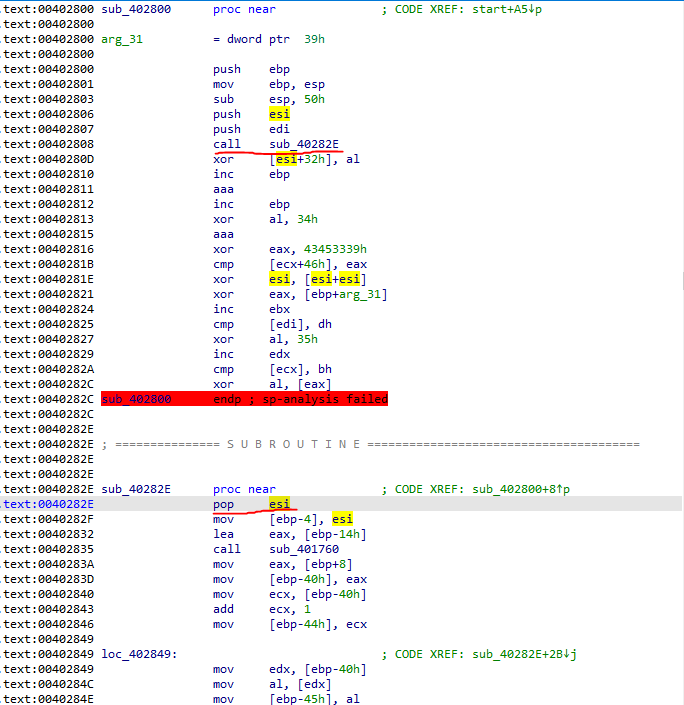
当程序执行sub_40282E时，sub_40282E函数没有进行正常的调节栈顶栈底操作，而是pop esi;，这将函数返回地址给pop出来了，程序将其放置在[ebp-4]中，这在程序之后会用到。

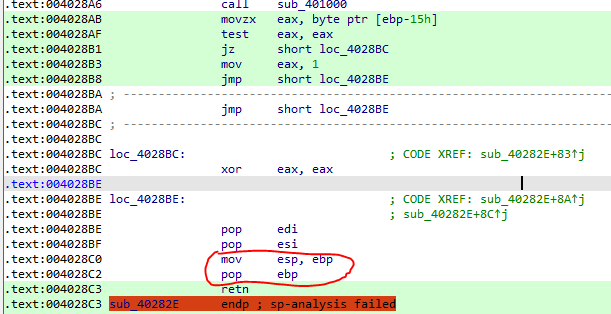
函数返回处

在看到sub_40282E的最后，它进行了调节栈顶栈底的操作，但函数开始时并没有其对应的操作，因此在这里它调节的是sub_40282E的上一级函数sub_402800函数的堆栈，它将堆栈还原成start函数（即程序主逻辑函数）调用sub_402800函数时的堆栈，而此时栈顶的值是sub_402800函数的返回地址。

程序通过这样子的逻辑跳过了调用sub_40282E函数需要再返回调用处的流程。

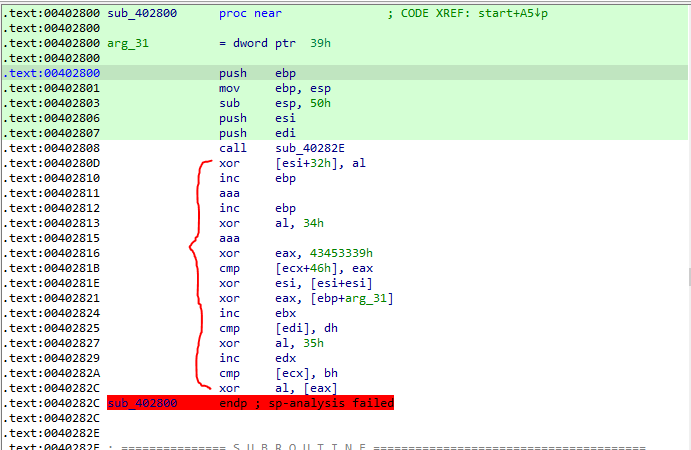
md5数据

上面说了这一部分是程序之后流程需要的数据，所以如果要想不干扰程序正常流程就不能改变它，但在这里为了获取伪代码，先将他nop掉，将sub_402800和sub_40282E连起来。

具体逻辑

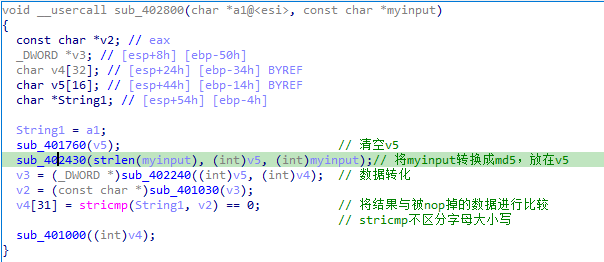
观察未nop的程序汇编就可以发现比较的字符串string1就是之前sub_40282E返回地址的那部分数据。

获取的数据

编写脚本

程序逻辑

获取用户输入，将{}中的内容提取出来；

根据输入，进行hanoi游戏，将每一块从大到小放置在第二列上；

将输入生成md5，进行比较；

hanoi初始状态和需要达到的状态：

数据形式

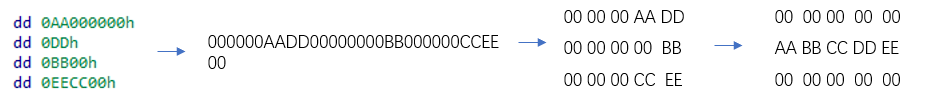
手动玩一下，得到流程：053254104123104524104，也可以找个脚本跑一下。

因为程序在switch时进行了与0xF相与再减一的操作，因此满足条件的字符串有很多，但最后需要字符串的md5与上面数据相同，即：0x30, 0x46, 0x32, 0x45, 0x37, 0x45, 0x34, 0x34, 0x37, 0x35,0x39, 0x33, 0x45, 0x43, 0x39, 0x41, 0x46, 0x33, 0x34, 0x36, 0x33, 0x45, 0x39, 0x43, 0x38, 0x37, 0x34, 0x35, 0x42, 0x38, 0x39 , 0x32。

脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
import hashlib
oper = "053254104123104524104"
oper = [int(i) + 1 for i in oper]
# 六种输入char对应六种case方法
# oper是符合条件输入的低位
# 符合条件的输入 为 oper 补足 它的高位
high_bit = [0x20, 0x30, 0x40, 0x50, 0x60, 0x70]
final = [
    0x30, 0x46, 0x32, 0x45, 0x37, 0x45, 0x34, 0x34, 0x37, 0x35,
    0x39, 0x33, 0x45, 0x43, 0x39, 0x41, 0x46, 0x33, 0x34, 0x36,
    0x33, 0x45, 0x39, 0x43, 0x38, 0x37, 0x34, 0x35, 0x42, 0x38,
    0x39, 0x32
]
final_s = "".join(chr(i) for i in final)
final_s = final_s.lower()
print(final_s)
for a in high_bit:
    for b in high_bit:
        for c in high_bit:
            for d in high_bit:
                for e in high_bit:
                    for f in high_bit:
                        now_oper = []
                        for i in oper:
                            match i:
                                case 1:
                                    now_oper.append(i + a)
                                case 2:
                                    now_oper.append(i + b)
                                case 3:
                                    now_oper.append(i + c)
                                case 4:
                                    now_oper.append(i + d)
                                case 5:
                                    now_oper.append(i + e)
                                case 6:
                                    now_oper.append(i + f)
                        now_str = "".join(chr(i) for i in now_oper)
                        md5 = hashlib.md5(now_str.encode())
                        result = md5.hexdigest()
                        if result == final_s:
                            print(now_str)